利用零点存在定理证明函数的零点个数是导数压轴题中的热点命题形式,同时也是考生不易掌握的难点部分. 当使用零点存在定理证明时,我们需要找到零点所在区间的界,需要取合适的区间界点,而取点的手段具有一定的难度与技巧性. 在考场上遇见时,短时间内难以想到合适的答案. 其实,虽然这一问题求解有困难,但并不是毫无规律. 本文将从取点的原理及手段入手,举例讲解破解零点问题的有效手段.
工作原理
设函数 $f(x)$ 在定义域上单调递增,且存在一个零点 $x=x_0$,已知该零点无法通过代数方法解出,则为了证明该函数在定义域上有零点,我们需要找到合适的上下界,证明函数值在两个界点处异号.
为了寻找一个点 $x=x_1$ 作为区间左端点,使 $f\left(x_1\right)<0$,我们需要找到一个函数 $g(x)$,设置如下要求:$g(x)>f(x)$,且 $g(x)$ 的零点 $x=x_1$ 可以通过代数方法解出. 那么,当 $x=x_1$ 时,必有 $x_1<x_0$,且 $f\left(x_1\right)<0$.
同理,为了寻找一个点 $x=x_2$ 作为区间右端点,使 $f\left(x_2\right)>0$, 我们也需要找到一个函数 $h(x)$,其中 $h(x)<f(x)$,且 $h(x)$ 有代数零点 $x=x_2$. 那么,当 $x=x_2$ 时,必有 $x_2>x_0$,且 $f\left(x_2\right)$ $>0$.
函数 $f(x)$ 在定义域上单调递减的情况同理.
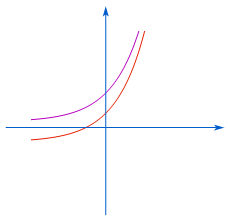
我们可以通过如下示意图来直观地理解这个原理. (仅绘出 $f(x)$ 单调递增的示意图,图象表示的是原函数零点附近的大致走势,并非全局的单调性)
![图片[1]-零点问题中取点技巧的多彩应用-小眼睛数学](https://xyj2000.cn/wp-content/uploads/2024/11/零点.png)
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END





暂无评论内容